알고리즘/이분 탐색
[BOJ] 백준 2143 - 두 배열의 합
송승현(SSH)
2023. 3. 30. 10:18
1. 문제
https://www.acmicpc.net/problem/2143
2143번: 두 배열의 합
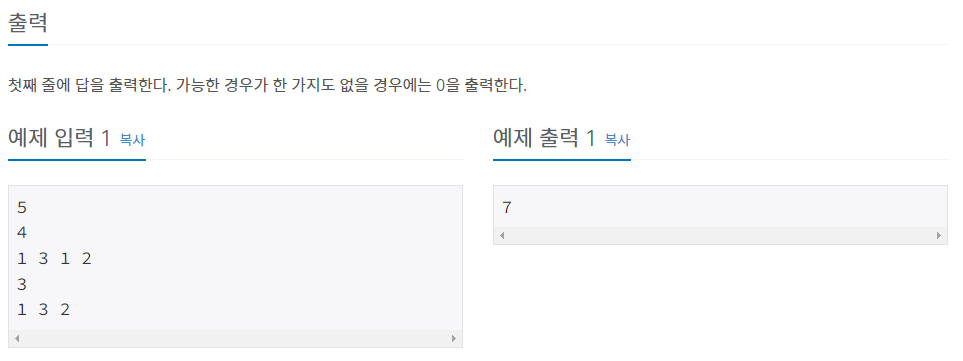
첫째 줄에 T(-1,000,000,000 ≤ T ≤ 1,000,000,000)가 주어진다. 다음 줄에는 n(1 ≤ n ≤ 1,000)이 주어지고, 그 다음 줄에 n개의 정수로 A[1], …, A[n]이 주어진다. 다음 줄에는 m(1 ≤ m ≤ 1,000)이 주어지고, 그
www.acmicpc.net

2. 풀이
- 배열의 모든 부분 집합을 구하여 값을 계산한다면, 배열 하나만 해도 시간 복잡도 $ O(2^n) $를 가지기 때문에 시간초과가 발생한다.
- 이 문제의 핵심 포인트는 "누적합"을 구하는 것이다.
- 그렇다면 A 배열과 B 배열의 누적합의 개수는 몇 개씩이 나올까??
- A 배열에서 누적합의 개수는 총 n개가 나온다.
- <예제 입력 1을 기준으로>
- 0번 인덱스 ~ 3번 인덱스까지의 누적합
- 1번 인덱스 ~ 3번 인덱스까지의 누적합
- 2번 인덱스 ~ 3번 인덱스까지의 누적합
- 3번 인덱스 ~ 3번 인덱스까지의 누적합
- B 배열에서 누적합의 개수는 총 m개가 나온다.
- <예제 입력 1을 기준으로>
- 0번 인덱스 ~ 2번 인덱스까지의 누적합
- 1번 인덱스 ~ 2번 인덱스까지의 누적합
- 2번 인덱스 ~ 2번 인덱스까지의 누적합
- 이제 A 배열의 누적합 원소 + B 배열의 누적합 원소가 T가 되는 경우만 카운트 해주면 답이 될 수 있다.
- 그러나 이를 2중 반복문으로 계산한다면 시간초과가 발생한다.
- 왜냐하면 누적합의 개수는 n개, m개가 나오지만, 실제로 값을 비교해야하는 원소의 개수는 n!개 ,m!개가 나오기 때문에 $ O(n^2) $으로 하면 당연히 시간 초과가 발생한다.
- 이를 해결하기 위해 Two Pointer로 해결하는 방법을 생각해보자
- A의 누적합 배열과 B의 누적합 배열을 오름 차순으로 정렬한 후, A의 누적합 배열의 0번 인덱스부터 탐색할 left 변수와 B의 누적합 배열의 마지막 인덱스부터 탐색할 right 변수를 만들고 초기화한다.
- while 문을 만드는 데, 이때의 조건은 left가 A의 누적합 배열의 끝까지 && B의 누적합 배열의 0번 인덱스까지 돌아야한다.
- 인덱스에 맞는 누적합 원소의 합을 구하면서 그 값이 T와 같은지 아닌지를 판단한다.
- 합이 T보다 큰 경우
- 합이 T 보다 큰 값이므로, 작은 값을 만들어주기 위해서는 right를 -1 해야 한다.
- 왜냐하면 left는 작은 값에서 올라오고 right는 큰 값에서 내려가기 때문에 right - 1을 해야 다음 합이 지금 합보다 작아질 수 있다.
- 합이 T보다 작은 경우
- 합이 T 보다 작은 값이므로, 큰 값을 만들어주기 위해서는 left + 1을 해야 한다.
- 합이 T와 같은 경우
- 합이 T와 같다면, 중복된 원소의 개수를 생각해야 한다.
- 중복된 원소가 아닐때 까지 반복을 돌고, 그 위치까지 result에 더해준다.
- 그리고 right와 left의 원소를 갱신한다.
- 합이 T보다 큰 경우

3. 소스코드
import java.io.*;
import java.util.ArrayList;
import java.util.Collections;
import java.util.List;
import java.util.StringTokenizer;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
// 만들어야 하는 수
int T = Integer.parseInt(br.readLine());
// A 배열의 개수
int aCnt = Integer.parseInt(br.readLine());
int[] aArr = new int[aCnt];
StringTokenizer st = new StringTokenizer(br.readLine());
for (int i = 0; i < aCnt; i++) {
aArr[i] = Integer.parseInt(st.nextToken());
}
// B배열의 개수
int bCnt = Integer.parseInt(br.readLine());
int[] bArr = new int[bCnt];
st = new StringTokenizer(br.readLine());
for (int i = 0; i < bCnt; i++) {
bArr[i] = Integer.parseInt(st.nextToken());
}
// 결과
long result = 0;
// A와 B의 누적합 리스트
List<Integer> aSumArrList = new ArrayList<>();
List<Integer> bSumArrList = new ArrayList<>();
// A의 누적합들을 구하여 리스트에 넣는다.
for (int i = 0; i < aCnt; i++) {
int old = 0;
for (int j = i; j < aCnt; j++) {
old += aArr[j];
aSumArrList.add(old);
}
}
// B의 누적합들을 구하여 리스트에 넣는다.
for (int i = 0; i < bCnt; i++) {
int old = 0;
for (int j = i; j < bCnt; j++) {
old += bArr[j];
bSumArrList.add(old);
}
}
// 투포인터 방식을 위한 정렬
Collections.sort(aSumArrList);
Collections.sort(bSumArrList);
// 투포인터 방식으로 T가 나오는 개수를 계산
int left = 0;
int right = bSumArrList.size() - 1;
long hap = 0;
while (left < aSumArrList.size() && right > -1) {
hap = aSumArrList.get(left) + bSumArrList.get(right);
// 합이 T와 같다면 a와 b 둘다 중복된 값이 안나올 때까지 개수를 세준다.
if (hap == T) {
// 현재 a리스트에서 탐색중인 값이 안나올때까지 반복문 계속
long aDupCnt = 0;
int aSelected = aSumArrList.get(left);
while (left < aSumArrList.size() && aSumArrList.get(left) == aSelected) {
aDupCnt++;
left++;
}
// 현재 b리스트에서 탐색중인 값이 안나올때까지 반복문 계속
long bDupCnt = 0;
int bSelected = bSumArrList.get(right);
while (right >= 0 && bSumArrList.get(right) == bSelected) {
bDupCnt++;
right--;
}
result += aDupCnt * bDupCnt;
} else {
if (hap > T) {
right -= 1;
} else {
left += 1;
}
}
}
bw.write(Long.toString(result));
bw.flush();
bw.close();
br.close();
}
}4. 배운점
- 누적합은 $ O(1) $로, Two Pointer는 $ O(n) $으로 구할 수 있다.