알고리즘/그래프
[BOJ] 백준 1937 - 욕심쟁이 판다
송승현(SSH)
2023. 4. 3. 16:03
1. 문제
https://www.acmicpc.net/problem/1937

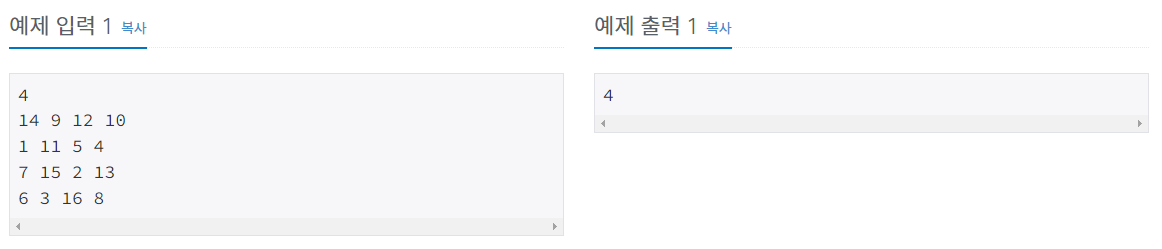
2. 풀이
- 모든 좌표에서 DFS를 실행하면 $O(N^2)$ x $O(N^2)$ -> $O(N^4)$ 으로 시간 초과가 발생
- DFS + DP를 이용하여 시간 복잡도를 줄일 수 있다.
dp[i][j] = r
map의 (i, j)에서 출발했을 때 최대 이동할 수 있는 칸의 개수 = r
- 판다가 어디에서 처음 풀어놔야 하는지도 정해야 하기 때문에 모든 좌표에서 DFS 함수를 출발시켜야 한다.($O(N^2)$)
- DFS 함수에서는 다음과 같은 로직을 수행한다.
- 출발하는 것도 움직인 것으로 보기 때문에 DFS 함수를 실행하면 dp[x][y] = 1을 통하여 움직임을 더해준다.
- 4방 탐색으로 좌표를 찾고 현재 내 위치의 대나무의 양보다 다음 위치의 대나무의 양이 더 많을 때 이동할 수 있다.
- 이 때 재귀를 가지치기 하기 위해서는 현재 좌표의 DP 값에는 현재 좌표의 DP 값과 이동했을 때의 DP 값 + 1 중 큰 값으로 넣어줘야 한다.
- 만약 DFS 함수를 타고 왔는데, 이 위치의 dp 값이 이미 0보다 큰 값이 나와있다는 것은 "다른 좌표가 이미 이 지점을 경유하여 최댓값을 갱신해놓은 상태"를 의미 하기 때문에 이 길로 더이상 탐색할 필요가 없다.
- 마지막으로 result에다 리턴받은 dp값의 최대값을 갱신해주면 정답이다.
3. 소스 코드
import java.io.*;
import java.util.StringTokenizer;
public class Main {
static int[][] map;
static int N;
static int[][] dp;
static int[] dx = {1, -1, 0, 0};
static int[] dy = {0, 0, 1, -1};
static int result = Integer.MIN_VALUE;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
// 입력을 변수 및 배열에 초기화
N = Integer.parseInt(br.readLine());
map = new int[N][N];
for (int i = 0; i < N; i++) {
StringTokenizer st = new StringTokenizer(br.readLine());
for (int j = 0; j < N; j++) {
map[i][j] = Integer.parseInt(st.nextToken());
}
}
// dp 배열 초기화
dp = new int[N][N];
// DFS 시작
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
result = Math.max(result, pandaDFS(i, j));
}
}
bw.write(Integer.toString(result));
bw.flush();
bw.close();
br.close();
}
private static int pandaDFS(int x, int y) {
// 지금 탐색하는 좌표를 거쳐간 경로의 최대 값(dp[x][y])이 0보다 크다는건 이미 이 지점을 지나갔을 때 최댓값을 갱신했다는 의미이므로
// dp[x][y] 값을 리턴한다.
if (dp[x][y] > 0) {
return dp[x][y];
}
// 좌표에 도착했다는건 한번 이동했다는 의미이므로 1을 넣는다.
dp[x][y] = 1;
for (int i = 0; i < 4; i++) {
int xf = x + dx[i];
int yf = y + dy[i];
if (isAvailable(xf, yf) && map[x][y] < map[xf][yf]) {
// 현재까지 DP 값과 다음 좌표로의 return + 1과 비교하여 dp 위치 값을 갱신한다.
dp[x][y] = Math.max(dp[x][y], pandaDFS(xf, yf) + 1);
}
}
return dp[x][y];
}
// 범위를 넘는지 판단하는 함수
private static boolean isAvailable(int x, int y) {
return x >= 0 && x < N && y >= 0 && y < N;
}
}4. 점수
- 80 / 100