알고리즘/다익스트라
[BOJ] 백준 1753 - 최단경로 풀이
송승현(SSH)
2023. 4. 4. 09:52
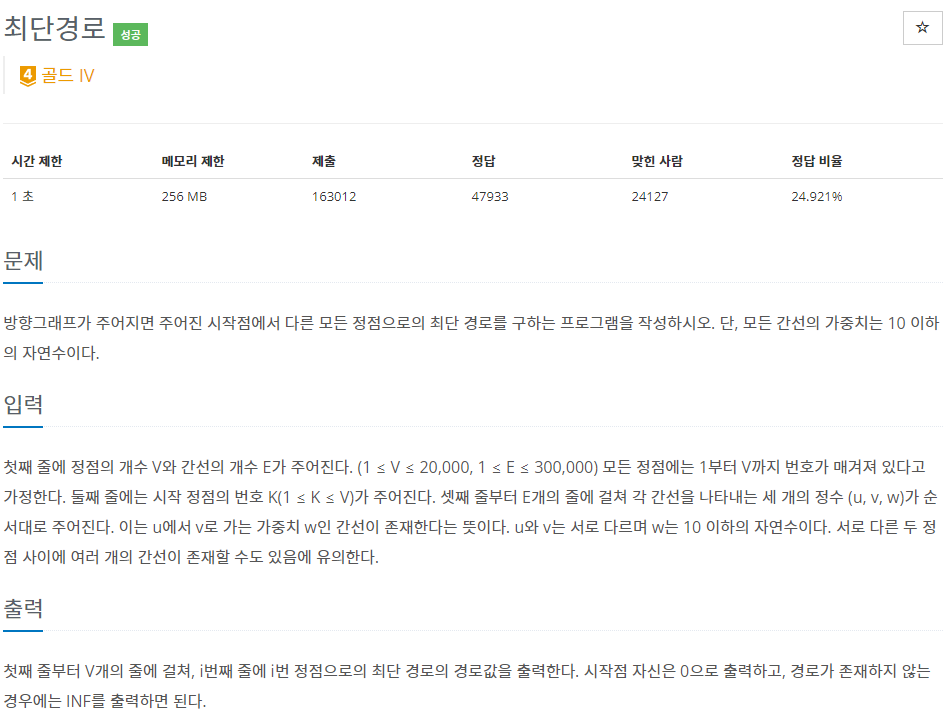
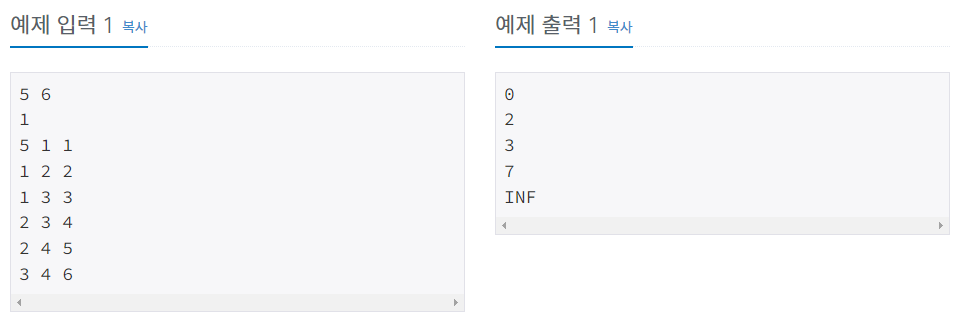
1. 문제
https://www.acmicpc.net/problem/1753
1753번: 최단경로
첫째 줄에 정점의 개수 V와 간선의 개수 E가 주어진다. (1 ≤ V ≤ 20,000, 1 ≤ E ≤ 300,000) 모든 정점에는 1부터 V까지 번호가 매겨져 있다고 가정한다. 둘째 줄에는 시작 정점의 번호 K(1 ≤ K ≤ V)가
www.acmicpc.net
2. 풀이
- 간선의 가중치가 10이하인 자연수이고 한 정점에서 다른 모든 정점까지의 최단 경로를 구하는 문제이기 때문에 다익스트라로 문제를 해결할 수 있다.
- 만약 다익스트라 코드를 작성하는 것이 아직 어렵다면 "최소 비용 구하기" 문제를 먼저 풀어보자
- https://sorryday.tistory.com/84
[BOJ] 백준 1916 - 최소비용 구하기
1. 문제 https://www.acmicpc.net/problem/1916 1916번: 최소비용 구하기 첫째 줄에 도시의 개수 N(1 ≤ N ≤ 1,000)이 주어지고 둘째 줄에는 버스의 개수 M(1 ≤ M ≤ 100,000)이 주어진다. 그리고 셋째 줄부터 M+2줄
sorryday.tistory.com
- 다익스트라 함수를 실행하고 D 배열을 탐색하면서 D 배열의 원소 값이 처음에 설정한 최대 값의 크기와 같다면 "INF"를 출력하고 다른 값이라면 그 값을 출력하면 정답이다.
3. 소스코드
import java.io.*;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Collections;
import java.util.Comparator;
import java.util.List;
import java.util.PriorityQueue;
import java.util.StringTokenizer;
public class Main {
static class Node {
int nV;
int nCost;
public Node(int nV, int nCost) {
this.nV = nV;
this.nCost = nCost;
}
}
static List<Node>[] inList; // 인접 리스트
static int V; // 총 정점의 개수
static int E; // 총 간선의 개수
static int startV; // 스타트 정점
static int[] D; // 최소 비용이 저장된 배열
static boolean[] visited; // 방문체크 배열
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
BufferedWriter bw = new BufferedWriter(new OutputStreamWriter(System.out));
// 입력
StringTokenizer st = new StringTokenizer(br.readLine());
V = Integer.parseInt(st.nextToken());
E = Integer.parseInt(st.nextToken());
startV = Integer.parseInt(br.readLine());
// 인접리스트 초기화
inList = new ArrayList[V + 1];
for (int i = 1; i <= V; i++) {
inList[i] = new ArrayList<>();
}
// 인접리스트 구성
for (int i = 0; i < E; i++) {
st = new StringTokenizer(br.readLine());
int from = Integer.parseInt(st.nextToken());
int to = Integer.parseInt(st.nextToken());
int cost = Integer.parseInt(st.nextToken());
inList[from].add(new Node(to, cost));
}
// 배열 선언
visited = new boolean[V + 1];
D = new int[V + 1];
Arrays.fill(D, Integer.MAX_VALUE / 4);
minCostDistDji();
// 결과 출력
for (int i = 1; i <= V; i++) {
if (D[i] == Integer.MAX_VALUE / 4) {
bw.write("INF" + "\n");
} else {
bw.write(D[i] + "\n");
}
}
bw.flush();
bw.close();
br.close();
}
// 다익스트라 함수
private static void minCostDistDji() {
// 우선순위 큐 선언
PriorityQueue<Node> pq = new PriorityQueue<>(new Comparator<Node>() {
@Override
public int compare(Node o1, Node o2) {
return o1.nCost - o2.nCost;
}
});
pq.add(new Node(startV, 0));
D[startV] = 0;
while (!pq.isEmpty()) {
Node n = pq.poll();
// 꺼낸 점이 방문한 점이면
if (!visited[n.nV]) {
visited[n.nV] = true;
}
// 인접한 리스트를 본다
for (int i = 0; i < inList[n.nV].size(); i++) {
// 인접한 점 꺼내기
Node getNode = inList[n.nV].get(i);
if (getNode != null && !visited[getNode.nV]) {
if (D[getNode.nV] > n.nCost + getNode.nCost) {
D[getNode.nV] = n.nCost + getNode.nCost;
pq.add(new Node(getNode.nV, D[getNode.nV]));
}
}
}
}
}
}4. 점수
90 / 100